Inverse Kinematics (IK)

The inverse kinematic problem
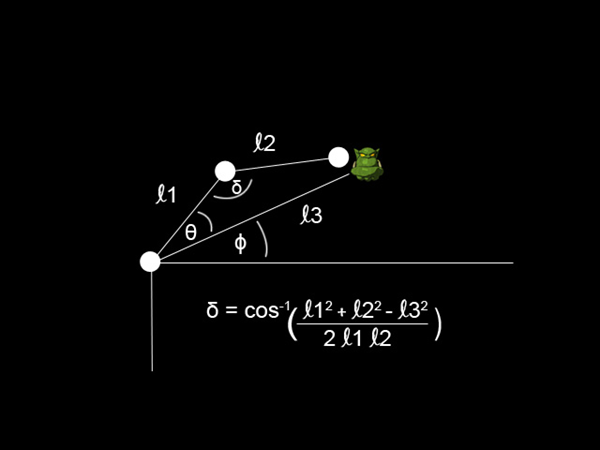
The inverse kinematic formula

The goal of this project was to see if IK would be a viable option for hand detection when using the kinect camera.
Inverse kinematics refers to the use of mathematical equations to determine the joint angles of a structure that provide a desired position of the end-effector.
In other words, you have a structure, such as a robotic arm, that has a base (or origin) and a point of significance (an end-effector), with the intention of moving the end-effector towards some goal. In order to determine the best way for an end-effector to reach its target location, a variety of mathematical calculations can be used to determine the best angles for each of the joints in the structure. There are many ways to perform these calculations, each with their own set of advantages and disadvantages.
The application I built in cpp, using the ORGE 3D framework, uses a simple method for calculating the IK values. In this application the Ogre's head is the target that can be moved by the user. A limb is represented as a series of lines and the spheres represent the joints. The end effector attempts to reach the target wherever the target may be.
Here is a brief overview of the project in the form of a Youtube video:
Articles I found helpful
If you are interested in more on the subject here are some articles I would recommend
Buss, S.R., (2004, Apr. 17). "Introduction to Inverse Kinematics with Jacobian Transpose Pseudoinverse and Damped Least Squares methods." [Online] Available: http://math.ucsd.edu/~sbuss/ResearchWeb/ikmethods/iksurvey.pdf
ElKoura, G., Singh, K., Handrix: Animating the Human Hand. In: Eurographics/SIGGRAPH Symposium on Computer Animation, pp. 110-119, 2003.
El-Sawah, A., Georganas, N.D., Petriu, E.M., Finger Inverse Kinematics Using Error Model Analysis for Gesture Enabled Navigation in Virtual Environments. In: IEEE International Workshop on HAV Environments and their Applications, pp. 34-39, 2006.
El-Sawah, A., Joslin, C., Georganas, N.D., Petriu, E.M. A Framework for 3D Hand Tracking and Gesture Recognition using Elements of Genetic Programming. In: Proc. of IEEE CRV, 2007, pp. 495-502.
Ghahramani, Z. An Introduction to Hidden Markov Models and Bayesian Networks. In: International Journal of Pattern Recognition and Artificial Intelligence, vol. 15, no. 1, pp. 9-42, 2001.
Johansson, G. Visual Perception of Biological Motion and a Model for its Analysis. In: Perception and Psychophysics, vol. 14, no. 2, pp. 201-211, 1973.
Joslin, C. , El-Sawah, A., Qing, C., Georganas, N. Dynamic Gesture Recognition. In IMTC 2005: Proceedings of the 2005 Instrumentation and Measurement Technology Conference. Discover Lab., Ottawa Univ., Ont., pp. 1706-1711.
Lathuiliere, F., and Herve, J.-Y. Visual tracking of hand posture with occlusion handling. In: Proc. 15th IEEE Int. Conf. Pattern Recog., vol. 3, pp. 1129–1133, 2000.
Lee, J., Kunii, T.L., Model-Based Analysis of Hand Posture, In: IEEE Computer Graphics and Applications, vol. 15, no. 5, pp. 77-86, 1995.
Lien, C., Huang, C., Model-Based Articulated Hand Motion Tracking for Gesture Recognition, In: Image and Vision Computing, vol. 16, pp.121-134, 1998.
Min, B., Yoon, H., Soh, J., Yang, Y., Ejima, T. Hand Gesture Recognition using Hidden Markov Models. In IEEE Intern’l Conf. on Systems, Man, and Cybernetics, vol.5, pp. 4232-4235, Oct. 1997.
Parent, Rick. Computer Animation: algorithms and techniques. Boston: Elsevier/Morgan Kaufmann, 2008.
Rijpkema, H., Girard, M., Computer Animation of Knowledge-Based Human Hand. In: SIGGRAPH Computer Graphics, vol. 25, no. 4, pp. 339-348, 1991.
Tran, C. , Trivedi, M. 3D Posture and Gesture Recognition for Interactivity in Smart Spaces. In: IEEE Transactions on Industrial Informatics. vol. 8, no. 1, pp. 178-187, Jan. 2012.
Tsang, W., Singh, K., Fiume, E. Helping Hand: An Anatomically Accurate Inverse Dynamics Solution for Unconstrained Hand Motion. In SCA '05: Proceedings of the 2005 ACM SIGGRAPH/Eurographics symposium on Computer animation. ACM, New York, NY, pp. 319-328.
Zhang, L., Hermanns, H., Jansen, D.N. Logic and Model Checking for Hidden Markov Models. In: Proc. 25th IFIP WG 6.1 International Conference on Formal Techniques for Networked and Distributed Systems, vol. 3731, pp. 98-112, 2005.